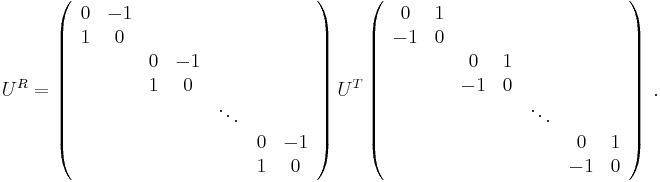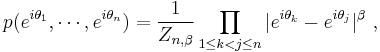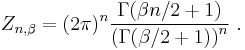Circular ensemble

In the theory of random matrices, the circular ensembles are measures on spaces of unitary matrices introduced by Freeman Dyson as modifications of the Gaussian matrix ensembles. The three main examples are the orthogonal circular ensemble (COE) on symmetric unitary matrices, the unitary circular ensemble (CUE) on unitary matrices, and the symplectic circular ensemble (CSE) on self dual unitary quaternionic matrices.

The distribution of the unitary circular ensemble CUE(n) is the Haar measure on the unitary group U(n). If U is a random element of CUE(n), then U^TU is a random element of COE(n); if U is a random element of CUE(2n), then U^RU is a random element of CSE(n), where

$U^R = \left( \begin{array}{ccccccc} 0 & -1 & & & & & \\ 1 & 0 & & & & & \\ & & 0 & -1 & & & \\ & & 1 & 0 & & & \\ & & & & \ddots & & \\ & & & & & 0& -1\\ & & & & & 1 & 0 \end{array} \right) U^T \left( \begin{array}{ccccccc} 0 & 1 & & & & & \\ -1 & 0 & & & & & \\ & & 0 & 1 & & & \\ & & -1 & 0 & & & \\ & & & & \ddots & & \\ & & & & & 0& 1\\ & & & & & -1 & 0 \end{array} \right)~.$

The joint distribution of eigenvalues of the circular ensembles is given by the probability density function

$p(e^{i\theta_1}, \cdots, e^{i \theta_n}) = \frac{1}{Z_{n,\beta}} \prod_{1 \leq k < j \leq n} |e^{i \theta_k} - e^{i \theta_j}|^\beta~,$

where β=1 for COE, β=2 for CUE, and β=4 for CSE. The normalisation constant Z_n,β is given by

$Z_{n,\beta} = (2\pi)^n \frac{\Gamma(\beta n/2 %2B 1)}{\left(\Gamma(\beta/2 %2B 1)\right)^n}~.$

Integrals of products of matrix coefficients in the unitary circular ensemble can be calculated using Weingarten functions.

References

Mehta, Madan Lal (2004), Random matrices, Pure and Applied Mathematics (Amsterdam), 142 (3rd ed.), Elsevier/Academic Press, Amsterdam, ISBN 978-0-12-088409-4, MR 2129906